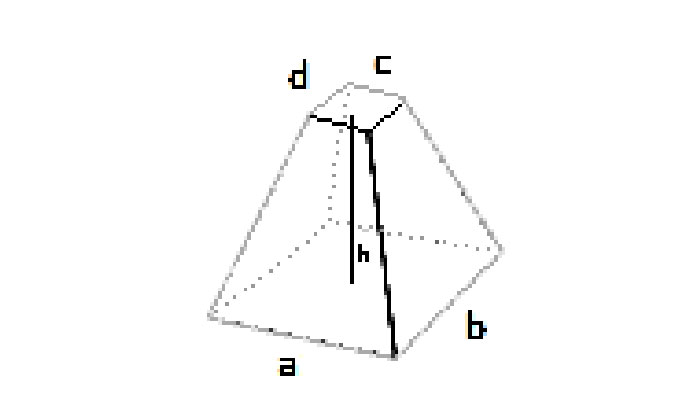
Calcolatore del Volume di un Piramide Troncata

Questo calcolatore online calcola il volume di un piramide tronca (frustum) sia per basi quadrate che rettangolari. Implementa la formula standard del volume del frustum con gestione coerente delle unità e controllo della precisione. Il metodo si basa sulla geometria classica (vedi Frustum – Volume), quindi i risultati sono matematicamente affidabili quando gli input sono validi (dimensioni non negative con la parte superiore/base nella stessa unità). Questo strumento è particolarmente utile in Italia, dove la progettazione architettonica e ingegneristica richiede spesso calcoli precisi per strutture complesse.

Calcolatore del Volume della Piramide Troncata

Cosa inserirai

Lato inferiore a

Lato superiore b

Altezza h

Unità

Decimali

Volume

—

Riepilogo Input

Formula

V = (h / 3) · (A_inferiore + A_superiore + √(A_inferiore · A_superiore))
Quadrato: A_inferiore=a², A_superiore=b² ⇒ V = (h/3)(a² + b² + ab)
Rettangolare: A_inferiore=L₁·W₁, A_superiore=L₂·W₂

La visualizzazione utilizza una proiezione assonometrica fissa: i rettangoli superiore e inferiore rimangono paralleli e centrati; gli spigoli verticali si scalano con la tua altezza. Le guide segnano L (blu), W (verde) e h (rosso).

Condividere questo?

Come Usare

Scegli la modalità Quadrata, Retangolare o Aree.
Inserisci:
- Quadrata: lato inferiore a, lato superiore b, altezza h.
- Retangolare: base L₁ × W₁, cima L₂ × W₂, altezza h.
- Aree: area inferiore A_bottom, area superiore A_top, altezza h.
Seleziona l’unità e la precisione decimale, quindi clicca su Calcola.
La visualizzazione riflette le tue proporzioni: blu ≈ lunghezza (L), verde ≈ larghezza (W), rosso ≈ altezza (h). La pillola qui sotto mostra i tuoi input per copia/incolla.

Formule

Volume generale del frustum

V = (h / 3) · (A_bottom + A_top + √(A_bottom · A_top))

Basi quadrate (lato inferiore a, lato superiore b):
A_bottom = a², A_top = b² ⇒ V = (h / 3) · (a² + b² + a·b)

Basi rettangolari (base L₁×W₁, cima L₂×W₂):
A_bottom = L₁·W₁, A_top = L₂·W₂ ⇒ V = (h / 3) · (L₁W₁ + L₂W₂ + √(L₁W₁·L₂W₂))

Controlli di sanità. Se la parte superiore è uguale a quella inferiore (A_top = A_bottom), la forma diventa un prisma e V = A_bottom·h. Se la parte superiore è 0, è una piramide completa e V = (A_bottom·h)/3.

Esempi Pre-calcolati (tutti gli input in cm; volumi in cm³)

Modalità	Dimensioni inferiori	Dimensioni superiori	h	Volume
Quadrata	a × a = 10 × 10	b × b = 6 × 6	12	784
Quadrata	a × a = 5 × 5	b × b = 5 × 5	8	200
Quadrata	a × a = 20 × 20	b × b = 10 × 10	15	3.500
Quadrata	a × a = 7.5 × 7.5	b × b = 3.2 × 3.2	18	542,94
Retangolare	L₁×W₁ = 12 × 8	L₂×W₂ = 6 × 4	20	1.120
Retangolare	L₁×W₁ = 50 × 40	L₂×W₂ = 30 × 20	35	43.113,5263
Retangolare	L₁×W₁ = 15 × 10	L₂×W₂ = 15 × 5	12	1.324,2641

Tutti i valori sono stati ricontrollati con V = (h/3)(A_bottom + A_top + √(A_bottomA_top)). L’arrotondamento è mostrato a 2–4 decimali dove utile.

Consigli Pratici & Controlli di Qualità

Mantieni le unità coerenti. Inserisci tutte le dimensioni lineari nella stessa unità; il calcolatore converte in volume in quella unità³ (ad es., cm → cm³).
Misura correttamente l’altezza. Usa la distanza perpendicolare tra le basi (non un bordo inclinato).
Usa la modalità Aree quando conosci già le aree delle basi (da disegni, CAD o misurazioni sul campo) per evitare di accumulare errori di arrotondamento.
Controllo di sanità con estremi: Se b → a, il risultato dovrebbe avvicinarsi a A·h. Se b → 0, il risultato dovrebbe avvicinarsi a (A·h)/3.
Controllo della precisione: Aumenta “Decimali” quando gli input sono piccoli o quando prevedi di concatenare calcoli (ad es., per la massa usando la densità).

CalcuLife.com